Unity Shader入门精要学习笔记:学习Shader所需的数学基础
前言
由于此章节部分内容博主已经在计算机图形学中学习过,所以会少记录一部分,可以前往图形学:上和图形学:下查看
笛卡尔坐标系
二维笛卡尔坐标系
一个二维笛卡尔坐标系包含两个部分的信息
- 原点
- 两条过原点的互相垂直的矢量,即x轴和y轴,这些坐标轴也被称为是该坐标系的基矢量。
OpenGL和DirectX使用了不同的二维笛卡尔坐标系。
三维笛卡尔坐标系
在三维笛卡尔坐标系中,我们需要定义三个坐标轴和一个原点。
这三个坐标轴被称为该坐标系的基矢量。通常情况下,这三个坐标轴之间是互相垂直的,且长度为1,这样的基矢量被称为标准正交基。但这并不是必须的。如果不都为1,就是正交基。
左手坐标系和右手坐标系
两种坐标系无法通过旋转做到重合。
左右手坐标系转换方法是,把其中一个轴反转,并保持其他两个轴不变。
Unity使用的坐标系
Unity使用的是左手坐标系。(模型空间)
在观察空间中,Unity使用的是右手坐标系。以摄像机为原点的坐标系。
点和矢量
点是n维空间中的一个位置,他没有大小,宽度这类概念。
矢量是指n维空间中一种包含了模和方向的有向线段。
单位矢量可以用类似:$\widehat a$来表示
矢量运算
零矢量不可以被归一化。
矢量的点积
公式一
几何意义:投影,这一点将会在下面的公式中得到解释。
- 性质一:点积可结合标量乘法
- 性质二:点积可结合标量加减法
- 性质三:一个矢量和本身进行点积的结果,是该矢量的模的平方
公式二
这个公式解释了投影原理
矢量的叉积
与点积不同的是,向量叉积的结果仍是一个矢量,而不是标量。
叉积不满足交换律,结合律。
矩阵
他有个更装逼的名字,叫母体。一个矩阵可以把一个矢量从一个坐标空间转换到另一个坐标空间。
特殊的矩阵
方块矩阵
行列树相同的矩阵
单位矩阵
转置矩阵
逆矩阵
如果一个矩阵有对应逆矩阵,我们就说这个矩阵是可逆的(非奇异的)。
正交矩阵
如果一个矩阵是正交的,那么它的转置矩阵和逆矩阵是一样的。
矩阵的几何意义:变换
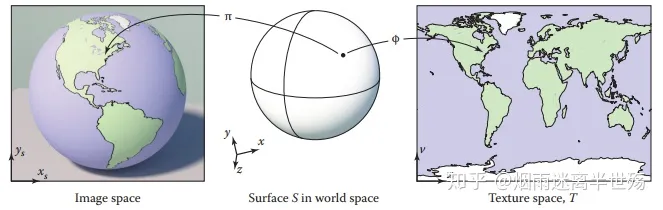
坐标空间
顶点的坐标空间变换过程
模型空间
模型空间也叫对象空间或者局部空间。
世界空间
多用于描述绝对位置
顶点变换第一步,就是将顶点坐标从模型空间变换到世界空间中,这个变换通常叫做模型变换。
观察空间
也被称为摄像机空间。
观察空间是一个三维空间,而屏幕空间是一个二维空间。
从观察空间到屏幕空间的转换需要经过一个操作,那就是投影。
顶点变换第二步,就是将顶点坐标从世界空间变换到观察空间中,这个变换通常叫做观察变换。
裁剪空间
顶点接下来要从观察空间转换到裁剪空间(齐次裁剪空间),这个用于变换的矩阵叫做裁剪矩阵,也被称为投影矩阵。
屏幕空间
经过投影矩阵变换后,我们可以进行裁剪操作,当完成了所有裁剪工作后,就需要进行真正的投影了,需要把视锥体投影到屏幕空间。
屏幕空间是一个二维空间,一次,我们需要把顶点从裁剪空间投影到屏幕空间中,来生成对应的2D坐标。
首先,我们要进行标准其次出发,也成为了透视除法。在OpenGL中我们把这一步得到的坐标叫做归一化的设备坐标(NDC)。
总结
顶点着色器的最基本的任务就是把顶点坐标从模型空间转换到裁剪空间中,在片元着色器中,我们通常也可以得到该片元在屏幕空间的像素位置。
法线变换
法线,也被称为法矢量,
Unity Shader的内置变量
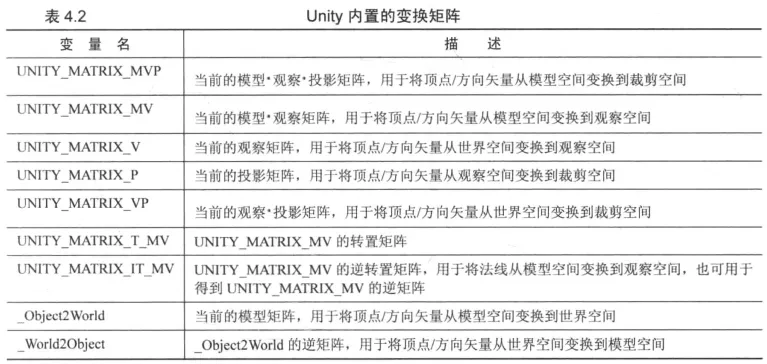
变换矩阵
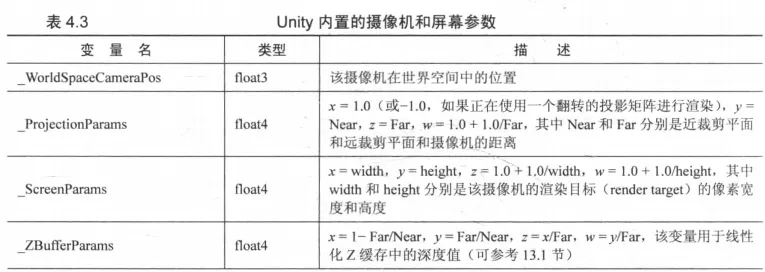
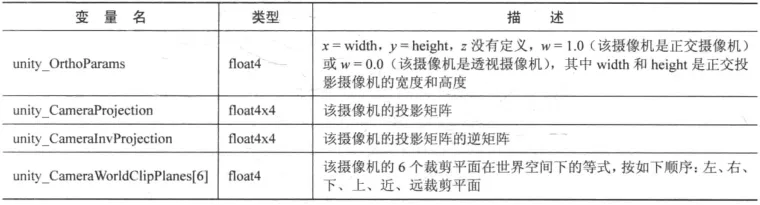
摄像机和屏幕参数
Unity中的屏幕坐标:ComputeScreenPos/VPOS/WPOS
VPOS是HLSL中对屏幕坐标的语义,而WPOS是CG中对屏幕坐标的语义。两者在UnityShader中时等价的。