图形学篇：Cohen-Sutherland直线段裁剪算法

前言

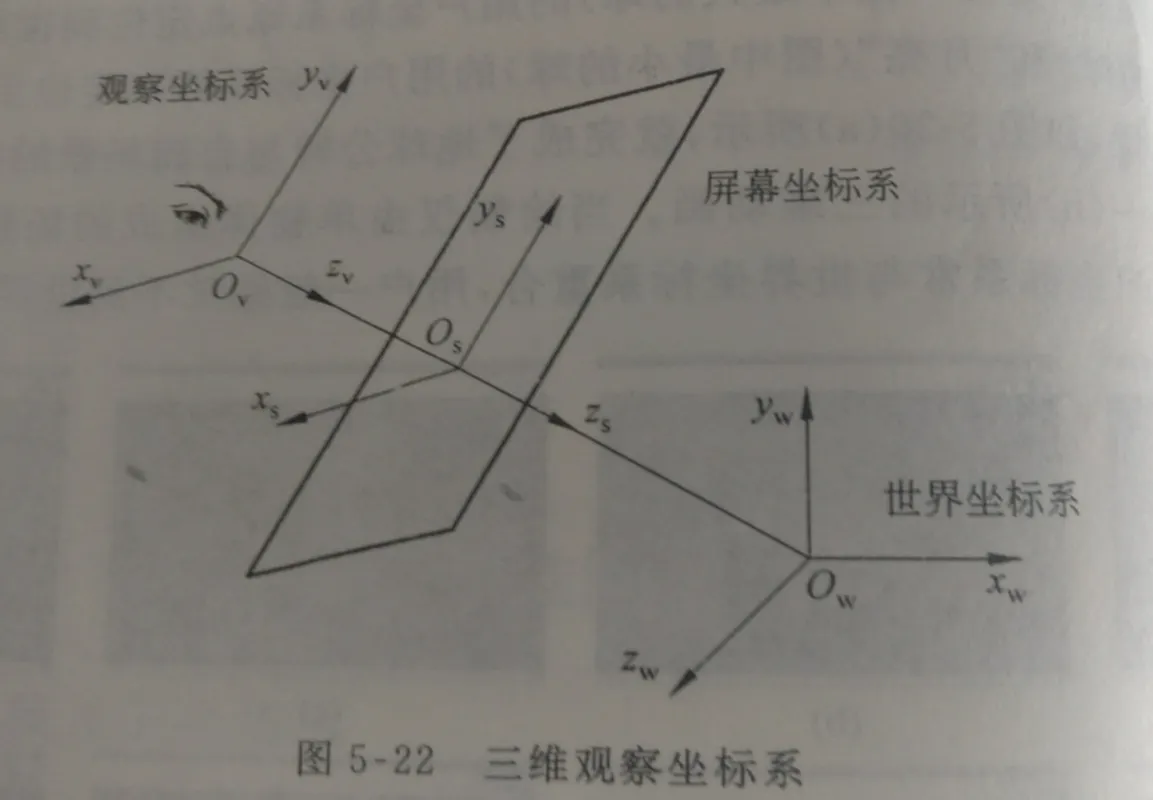
在二维观察中，需要在观察坐标系下根据窗口边界对世界坐标系中的二维图形进行裁剪，只将位于窗口内的图形变换到视区输出。直线裁剪是二维图形裁剪的基础，裁剪的实质是判断直线段是否与窗口边界相交，如相交则进一步确定直线段上位于窗口内的部分。

编码原理

Cohen-Sutherland直线段裁剪算法是最早流行的编码算法。每段直线段的断点都被赋予一组4位的二进制代码，称为区域编码,用来表示直线端点相对于窗口边界及其延长线的位置。假设窗口是标准矩形，由上(y=Wyt)下（y=Wyb）左（x=Wxl）右(x=Wxt)4条边界组成。延长窗口的4条边界形成9个区域这样根据直线的任意端点所处的窗口区域位置，可以赋予一组4位二进制区域码RC=C3C2C1C0,依次为上下左右边界为了保证窗口内及窗口边界上直线段端点的编码为0，我们做如下约定 C3：若y>Wyt,C3=1 C2：若y<Wyb,C2=1 C1：若y>Wxr,C1=1 C0：若y>Wxl,C0=1 也就有了如下代码

#define LEFT   1   //代表:0001
#define RIGHT  2   //代表:0010
#define BOTTOM 4   //代表:0100
#define TOP    8   //代表:1000
void EnCode(CP2 &pt)//端点编码函数, 实现函数体
{
    pt.rc = 0;
    if (pt.x < Wxl) {
        pt.rc = pt.rc  LEFT;
    }
    else if (pt.x > Wxr)
    {
        pt.rc = pt.rc  RIGHT;
    }
    if (pt.y < Wyb)
    {
        pt.rc = pt.rc  BOTTOM;
    }
    else if (pt.y > Wyt)
    {
        pt.rc = pt.rc  TOP;
    }
}