二维变换与裁剪

图形几何变换基础

规范化齐次坐标

为了使图形几何变换表达为图形顶点集合矩阵与某一变化矩阵相乘的问题，引入了规范化齐次坐标。
所谓齐次坐标就是用n+1维矢量表示n维矢量。
例如在三维空间中点P(x,y,z)\mathrm P\left(\mathrm x,\mathrm y,\mathrm z\right)的齐次坐标表示为(wx,wy,wz,w)\left(wx,wy,wz,w\right)，这里，w为任意不为0的比例系数，如果w=1就是规范化的齐次坐标。
定义了规范化其次坐标以后，图形的几何变换可以表示为图形顶点集合的规范换齐次坐标矩阵与某一变换矩阵相乘的形式。

矩阵相乘

矩阵相乘最重要的方法是一般矩阵乘积。它只有在第一个矩阵的列数（column）和第二个矩阵的行数（row）相同时才有意义。一般单指矩阵乘积时，指的便是一般矩阵乘积。一个m×n的矩阵就是m×n个数排成m行n列的一个数阵。由于它把许多数据紧凑的集中到了一起，所以有时候可以简便地表示一些复杂的模型。
设A为m×p的矩阵，B为p×n的矩阵，那么称m×n的矩阵C为矩阵A与B的乘积，记作C =A×B，其中矩阵C中的第i行第j列元素可以表示为：

(AB)ij=∑K=1Paikbkj=ai1b1j+ai2b2j+⋯+aipbpj{\left(AB\right)}_{ij}=\sum_{K=1}^Pa_{ik}b_{kj} = a_{i1}b_{1j}+a_{i2}b_{2j}+\dots+a_{ip}b_{pj}

如下所示

A=[a1a2a3a4a5a6]A=\begin{bmatrix}a_1&a_2&a_3\\a_4&a_5&a_6\end{bmatrix}

B=[b1b2b3b4b5b6]B=\begin{bmatrix}b_1&b_2\\b_3&b_4\\b_5&b_6\end{bmatrix}

C=AB=[a1b1+a2b3+a3b5a1b2+a2b4+a3b6a4b1+a5b3+a6b5a4b2+a5b4+a6b6]C=AB=\begin{bmatrix}a_1b_1+a_2b_3+a_3b_5&a_1b_2+a_2b_4+a_3b_6\\a_4b_1+a_5b_3+a_6b_5&a_4b_2+a_5b_4+a_6b_6\end{bmatrix}

二维几何变换矩阵

用规范化齐次坐标表示的二维图形几何变换矩阵是一个3x3的方阵，简称为二维几何变换矩阵。

T=[abpcdqlms]{T=\begin{bmatrix}a&b&p\\c&d&q\\l&m&s\end{bmatrix}}

从功能上可以把二维变换矩阵T分为4个子矩阵。
其中T1=[abcd]T_1=\begin{bmatrix}a&b\\c&d\end{bmatrix}是对图形进行比例，旋转，反射和错切变换。
T2=[lm]T_2=\begin{bmatrix}l&m\end{bmatrix}是对图形进行平移变换。
T3=[pq]T_3=\begin{bmatrix}p\\q\end{bmatrix}是对图形进行投影变换。
T4=[s]T_4=\left[s\right]是对图形进行整体比例变换。

物体变换与坐标变换

同一种变换可以看成物体变换，也可以看成坐标变换。
物体变换是使用同一变换矩阵作用于物体上的所有顶点，但坐标系位置不发生改变。
坐标变换是坐标系发生变换，但物体位置不发生改变，然后在新坐标系下表示物体上的所有顶点。
这两种变换紧密联系，各有各的优点，只是变换矩阵略有差异而已。

二维图形基本几何变换矩阵

二维图形的基本几何变换是指相对于坐标原点和坐标轴进行的几何变换，包括平移，比例，旋转，反射和错切5种变换。
物体变换是通过变换物体上每一个顶点实现的。
二维坐标点的基本几何变换可以表示为P′=P⋅TP'=P\cdot T的形式，其中P(x,y)P\left(x,y\right)为变换前的二维坐标点，P′(x′,y′)P'\left(x',y'\right)为变换后的二维坐标点，T为3x3的变换矩阵。

平移变换矩阵

将x在x轴方向移动TxT_x，将y在y轴方向移动TyT_y。

T=[100010TxTy1]T=\begin{bmatrix}1&0&0\\0&1&0\\T_x&T_y&1\end{bmatrix}

比例变换矩阵

P(x,y)P\left(x,y\right)相对于坐标原点O，沿x方向缩放SxS_x倍，沿y方向缩放SyS_y倍。

T=[Sx000Sy0001]T=\begin{bmatrix}S_x&0&0\\0&S_y&0\\0&0&1\end{bmatrix}

旋转变换矩阵

P(x,y)P\left(x,y\right)相对于坐标原点O旋转一个角度β\beta（逆时针方向为正，顺时针方向为负），得到P′(x′,y′)P'\left(x',y'\right)点的过程。

T=[cos⁡(β)sin⁡(β)0−sin⁡(β)cos⁡(β)0001]T=\begin{bmatrix}\cos\left(\beta\right)&\sin\left(\beta\right)&0\\-\sin\left(\beta\right)&\cos\left(\beta\right)&0\\0&0&1\end{bmatrix}

反射变换矩阵

反射变换也称对称变换，是P(x,y)P\left(x,y\right)点关于原点或者某个坐标轴反射得到P′(x′,y′)P'\left(x',y'\right)点的过程。

关于原点的二维反射变换矩阵

T=[−1000−10001]T=\begin{bmatrix}-1&0&0\\0&-1&0\\0&0&1\end{bmatrix}

关于x轴的二维反射变换矩阵

T=[1000−10001]T=\begin{bmatrix}1&0&0\\0&-1&0\\0&0&1\end{bmatrix}

关于y轴的二维反射变换矩阵

T=[−100010001]T=\begin{bmatrix}-1&0&0\\0&1&0\\0&0&1\end{bmatrix}

错切变换矩阵

P(x,y)P\left(x,y\right)沿x轴和y轴发生不等量的变换，得到P′(x′,y′)P'\left(x',y'\right)点的过程。

T=[1b0c10001]T=\begin{bmatrix}1&b&0\\c&1&0\\0&0&1\end{bmatrix}

二维图形复合变换

二维图形复合变换原理

负荷变化呢是指图形做了一次以上的基本几何变换，是基于几何变换的组合方式，复合变换矩阵是基本几何变换矩阵的组合。

P′  =  PT  =  P∏k=1nTkP'\;=\;PT\;=\;P\prod_{k=1}^nT_k

其中T为而为符合变换矩阵，T1⋯TnT_1\cdots T_n为n个单次二维基本变换矩阵的组合。
注意，矩阵相乘不满足乘法交换律！

相对于任意参考点的二维几何变换

二维基本几何变换是相对于坐标原点进行的平移，比例，旋转，反射和错切这五种变换，但在实际应用中常会遇到参考点不在坐标原点的情况，而比例变换和旋转变换是与参考点相关的。
相对于任意参考点的比例变换和旋转变换应表达为复合变换形式，变换方法为首先将参考点平移到坐标原点，对坐标原点进行比例变换或旋转变换，然后再进行反平移将参考点平移回原位置。

相对于任意方向的二维几何变换

二维基本几何变换是相对于坐标原点进行的平移，比例，旋转，反射和错切这五种变换，但在实际应用中常会遇到变换方向不与坐标轴重合的情况。
相对于任意方向的变换方法是首先对任意方向做旋转变换，使该方向与坐标轴重合，然后对坐标轴进行二维基本几何变换，最后做反向旋转变换，将任意方向还原到原来的方向。

二维图形裁剪

图形学中常用的坐标系

世界坐标系

描述现实世界中场景的固定坐标系称为世界坐标系（WCS）。
实数域坐标系。
三维世界直角坐标系可分为右手坐标系和左手坐标系两种。

用户坐标系

描述物体几何模型的坐标系称为用户坐标系（UCS），有时也称为局部坐标系（LCS）。
实数域坐标系。
用户坐标系是可移动坐标系，用户坐标系的原点可以放在物体的任意位置上，坐标系也可以旋转任意角度。

观察坐标系

观察坐标系（VCS）是在世界坐标系中定义的直角坐标系。
二维观察坐标系主要用于指定图形的输出范围。
三维观察坐标系是左手系，原点位于视点OvO_v，zvz_v轴垂直于屏幕，正向为视线方向。

屏幕坐标系

屏幕坐标系是（SCS）为实数域二维直角坐标系。
原点位于屏幕中心，xsx_s轴水平向右，ysy_s轴垂直向上为正。
在三维真实感场景中，为了反映物体的深度信息，常采用实数域三维屏幕坐标系。
三维屏幕坐标系是左手系，原点位于屏幕中心，zsz_s轴方向沿着视线方向，ysy_s轴垂直向上为正向，xsx_s轴与ysy_s轴和yzsyz_s轴成左手系。
只有采用三维屏幕坐标系才能正确反映物体上点的深度信息。

设备坐标系

显示器等图形输出设备自身都带有一个二维直角坐标系称为设备坐标系（DCS）。

窗口与视区

在观察坐标系中定义的确定显示内容的矩形区域称为窗口。
在屏幕坐标系中定义的输出图形的矩形区域称为视区。

窗视变换矩阵

T  =  [Sx000Sy0uxl−wxlSxuyb−wybSy1]T\;=\;\begin{bmatrix}S_x&0&0\\0&S_y&0\\{\mathfrak u}_{xl}-{\mathcal w}_{xl}S_x&{\mathfrak u}_{yb}-{\mathcal w}_{yb}S_y&1\end{bmatrix}

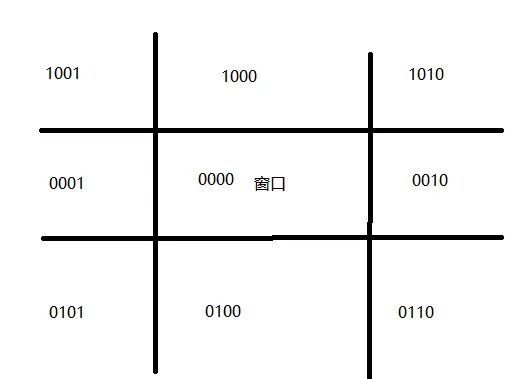
Cohen-Sutherland直线段裁剪算法

https://www.lfzxb.top/graphicslearning-cohen-sutherland/

中点分割直线段裁剪算法

中点分割算法和Cohen-Sutherland直线段裁剪算法比较

Cohen-Sutherland直线段裁剪算法提出对直线段与窗口的位置关系划分为3种情况，对于前两种情况进行了“简取”和“简弃”的处理，对于第三种情况，需要计算直线段与窗口边界的交点。重点分割直线段裁剪算法对第三种情况进行了改进，不需要求解直线段与窗口边界的交点就可以对直线段进行裁剪。

中点分割算法原理

直线段重点分割裁剪算法是采用二分算法的思想来逐次计算直线段的中点P以逼近窗口边界，设定控制常熟c为一个很小的数，当∣PP0∣\left|PP_0\right|或∣PP1∣\left|PP_1\right|小于控制常熟c时，中点收敛于直线段与窗口的交点。
中点分割裁剪算法的计算过程只用到了加法和移位运算，易于使用硬件实现。

三维变换与投影

三维图形几何变换

T=[abcpdefqghirlmns]T=\begin{bmatrix}a&b&c&p\\d&e&f&q\\g&h&i&r\\l&m&n&s\end{bmatrix}

T1=[abcdefghi]T_1=\begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}对物体进行比例，旋转，反射和错切变换
T2=[lmn]T_2=\begin{bmatrix}l&m&n\end{bmatrix}对物体进行平移变换
T3=[pqr]T_3=\begin{bmatrix}p\\q\\r\end{bmatrix}对物体进行投影变换
T4=[s]T_4=\left[s\right]对物体进行整体比例变换

三维图形基本几何变换矩阵

平移变换

T=[100001000010TxTyTz1]T=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\T_x&T_y&T_z&1\end{bmatrix}

比例变换

T=[Sx0000Sy0000Sz00001]T=\begin{bmatrix}S_x&0&0&0\\0&S_y&0&0\\0&0&S_z&0\\0&0&0&1\end{bmatrix}

旋转变换

三维旋转变换一般看做是二维旋转变换的组合，绕z轴旋转，满足右手螺旋法则；大拇指指向旋转轴正向，四指的转向为转角正向。β\beta为正向旋转角

绕x轴旋转

T=[10000cos⁡(β)sin⁡(β)00−sin⁡(β)cos⁡(β)00001]T=\begin{bmatrix}1&0&0&0\\0&\cos\left(\beta\right)&\sin\left(\beta\right)&0\\0&-\sin\left(\beta\right)&\cos\left(\beta\right)&0\\0&0&0&1\end{bmatrix}

绕y轴旋转

T=[cos⁡(β)0−sin⁡(β)00100sin⁡(β)cos⁡(β)00001]T=\begin{bmatrix}\cos\left(\beta\right)&0&-\sin\left(\beta\right)&0\\0&1&0&0\\\sin\left(\beta\right)&&\cos\left(\beta\right)&0\\0&0&0&1\end{bmatrix}

绕z轴旋转

T=[cos⁡(β)sin⁡(β)00−sin⁡(β)cos⁡(β)0000100001]T=\begin{bmatrix}\cos\left(\beta\right)&\sin\left(\beta\right)&0&0\\-\sin\left(\beta\right)&\cos\left(\beta\right)&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

反射变换

三维反射可以分为关于坐标轴反射和关于坐标情面的反射两类。

关于x轴反射

T=[10000−10000−100001]T=\begin{bmatrix}1&0&0&0\\0&-1&0&0\\0&0&-1&0\\0&0&0&1\end{bmatrix}

关于y轴反射

T=[−1000010000−100001]T=\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\end{bmatrix}

关于z轴反射

T=[−10000−10000100001]T=\begin{bmatrix}-1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

关于xOy轴反射

T=[1000010000−100001]T=\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&-1&0\\0&0&0&1\end{bmatrix}

关于yOz轴反射

T=[−1000010000100001]T=\begin{bmatrix}-1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

关于xOz轴反射

T=[10000−10000100001]T=\begin{bmatrix}1&0&0&0\\0&-1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

错切变换

T=[1bc0d1f0gh100001]T=\begin{bmatrix}1&b&c&0\\d&1&f&0\\g&h&1&0\\0&0&0&1\end{bmatrix}

三维错切变换中，一个坐标的变化受另外两个坐标变化的影响。
比如
如果变换矩阵第一列中元素d和g不为0，产生沿x轴方向的错切。
如果变换矩阵第二列中元素b和h不为0，产生沿y轴方向的错切。
如果变换矩阵第二列中元素c和f不为0，产生沿z轴方向的错切。
即，如果想让坐标往某个轴错切，其余轴相关元素为0即可。

坐标系变换

在实际应用中，经常需要将物体的描述从一个坐标变换到另一个坐标系。
例如在进行三维观察时，需要将物体的描述从世界坐标系变换到观察坐标系，然后通过旋转视点可以观察物体的全貌。同一种变换即可以看做点变换，也可以看做是坐标系变换。
点变换是物体上点的位置发生改变，但坐标系位置固定不动。
坐标系变换是建立新坐标系描述旧坐标系内的顶点，坐标系位置发生改变，但物体顶点位置固定不动。

二维坐标系变换

平移变换矩阵
$$T=\begin{bmatrix}1&0&0\\0&1&0\\-T_x&-T_y&1\end{bmatrix}$$
旋转变换矩阵

T=[cos⁡(β)−sin⁡(β)0sin⁡(β)cos⁡(β)0001]T=\begin{bmatrix}\cos\left(\beta\right)&-\sin\left(\beta\right)&0\\\sin\left(\beta\right)&\cos\left(\beta\right)&0\\0&0&1\end{bmatrix}

反射变换矩阵

同点反射

三维坐标系变换

规则同二维坐标系变换

平行投影

平行投影概念

由于显示器只能用二维图形表示三维物体，因此三维物体就要考投影来降低维数得到二维平面图形。
投影就是从投影中心发出射线，经过三维物体的每一点后，与投影面相交所形成的交点集合，因此把三维坐标转变为二维坐标的过程称为投影变换。

平行投影的分类

根据投影中心与投影面之间的距离的不同，投影可分为平行投影和透视投影。
投影中心到投影面的距离为有限值时得到的投影称为透视投影，若此距离无限大，则投影为平行投影。

透视投影

正透视投影要求存在一条投影中心线垂直于投影面，且其他投影线对称于投影中心线，否则为斜透视投影。

平行投影

投影方向不垂直于投影面的平行投影称为斜投影，投影方向垂直于投影面的平行投影称为正投影。
正投影最大的特点就是无论物体距离视点（眼睛或摄像机）多远，投影后的物体尺寸保持不变。常用于绘制物体的三视图。
投影分类如图

正交投影矩阵

T  =  [1000010000000001]T\;=\;\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}

三视图

主视图

将物体向yOz面做正投影

TV=TyOz  =  [0000010000100001]T_V=T_{yOz}\;=\;\begin{bmatrix}0&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

俯视图

将物体向xOz面做正投影

TV=TxOz  =  [1000000000100001]T_V=T_{xOz}\;=\;\begin{bmatrix}1&0&0&0\\0&0&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}

侧视图

将物体向xOy面做正投影

TV=TxOy  =  [1000010000000001]T_V=T_{xOy}\;=\;\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&0\\0&0&0&1\end{bmatrix}

透视投影

与平行投影想比，透视投影最大的特点是所有投影线都从空间一点（称为视点或投影中心）投射，离视点近的物体投影大，离视点远的物体投影小，小到极点消失，称为灭点。
透视投影模拟了人眼观察物体的过程，符合视觉习惯，所以在真实感图形中得到广泛应用
一般将屏幕放在观察者与物体之间。
投影线与屏幕的交点就是物体上一点的透视投影。观察者的眼镜位置称为视点，垂直于屏幕的视线（中心视线）与屏幕的交点称为视心。
视点到视心的距离称为视距（如果放置摄像机，称为焦距）。
视点到物体的距离称为视径.
视点代表人眼，照相机，或摄像机的位置，是观察坐标系的原点。
视心是屏幕坐标系的原点。

透视投影分类

一点透视

当屏幕仅与一个坐标轴相交时，形成一个灭点，透视投影图为一点透视图。
一点透视变换矩阵为

T1  =  [10000100000−1d000Rd]T_1\;=\;\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&0&-\frac1d\\0&0&0&\frac Rd\end{bmatrix}

二点透视

当屏幕仅与两个坐标轴相交时，形成两个灭点，透视投影图为二点透视图。
二点透视变换矩阵为

T2  =  [2200−22d0100−2200−22d000Rd]T_2\;=\;\begin{bmatrix}\frac{\sqrt2}2&0&0&\frac{-\sqrt2}{2d}\\0&1&0&0\\\frac{-\sqrt2}2&0&0&-\frac{\sqrt2}{2d}\\0&0&0&\frac Rd\end{bmatrix}

三点透视

三点透视图是屏幕与3个坐标轴都相交时的透视投影图
三点透视变换矩阵为

T2  =  [22−120−12d02200−22−120−12d000Rd]T_2\;=\;\begin{bmatrix}\frac{\sqrt2}2&-\frac12&0&-\frac1{2d}\\0&\frac{\sqrt2}2&0&0\\\frac{-\sqrt2}2&-\frac12&0&-\frac1{2d}\\0&0&0&\frac Rd\end{bmatrix}