深度优先遍历 (DFS)

深度优先遍历，也称作深度优先搜索，缩写为DFS

深度优先遍历从某个顶点出发，访问此顶点，然后从v的未被访问的邻接点触发深度优先便利图，直至所有和v有路径想通的顶点都被访问到。

这样我们一定就访问到所有结点了吗，没有，可能还有的分支我们没有访问到，所以需要回溯（一般情况下都设置一个数组，来记录顶点是否访问到，如果访问到就不执行DFS算法，如果未被访问过就执行DFS算法）

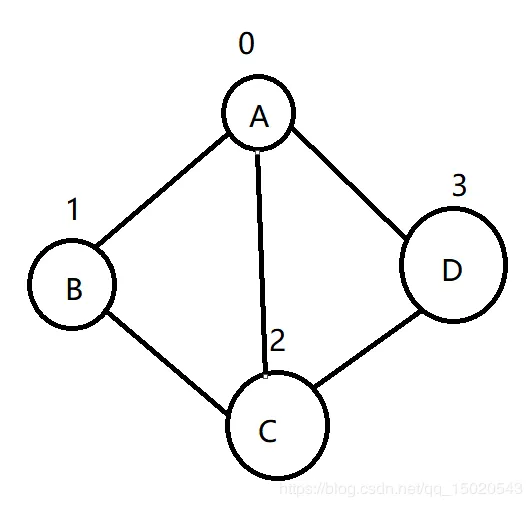
以这张图为例

我们约定，在没有碰到重复顶点的情况下，优先选择右手边

那么按深度优先遍历就是：A B C D E F G H(此时这条线路已经走到尽头，可是还有一个I顶点没有遍历，所以回到G，发现G的邻接点都遍历过了，再回到F，发现F的邻接点也都遍历过了。。。直到D顶点，发现I这个顶点没有遍历，所以把I再遍历，继续回溯，最终回到起点A) I

落实到代码就是

1
2
3
 
//访问标志的数组,为1表示访问过，为0表示未被访问
int visted[100];
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
 //邻接表的深度优先遍历算法
void AdjacencyList::DFS(GraphAdjList *G, int i) {
    EdgeNode *p;
    visted[i] = 1;
    cout << G->adjList[i].data << "--";
    p = G->adjList[i].firstedge;
    while (p)
    {
        if (!visted[p->adjvex])
        {
            //递归访问
            DFS(G, p->adjvex);
        }
        p = p->next;
    }

}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
 //邻接表的深度遍历操作
void AdjacencyList::DFSTraverse(GraphAdjList *G) {
    //初始化所有顶点都没有访问过
    cout<<"深度优先遍历结果为："<<endl;
    for (int i = 0; i < G->numVertexes; i++)
    {
        visted[i] = 0;
    }
    for (int i = 0; i < G->numVertexes; i++)
    {
        if (visted[i] == 0)
        {
            DFS(G, i);
        }
    }
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
 //
// Created by 烟雨迷离半世殇 on 2018/11/21.
//

#include <iostream>

using namespace std;

//访问标志的数组,为1表示访问过，为0表示未被访问
int visted[100];
//边表结点
typedef struct EdgeNode {
    //顶点对应的下标
    int adjvex;
    //指向下一个邻接点
    struct EdgeNode *next;
} edgeNode;

//顶点表结点
typedef struct VertexNode {
    //顶点数据
    char data;
    //边表头指针
    edgeNode *firstedge;
} VertexNode, AdjList[100];

//集合
typedef struct {
    AdjList adjList;
    //顶点数和边数
    int numVertexes, numEdges;
} GraphAdjList;

class AdjacencyList {
public:

    void CreateALGraph(GraphAdjList *G);

    void ShowALGraph(GraphAdjList *G);

    void DFS(GraphAdjList *G, int i);

    void DFSTraverse(GraphAdjList *G);

    void Test();


};

void AdjacencyList::CreateALGraph(GraphAdjList *G) {
    int i, j, k;
    edgeNode *e;
    cout << "输入顶点数和边数" << endl;
    //输入顶点数和边数
    cin >> G->numVertexes >> G->numEdges;
    //读入顶点信息，建立顶点表
    for (i = 0; i < G->numVertexes; i++)
    {
        //输入顶点信息
        cin >> G->adjList[i].data;
        //将边表置为空表
        G->adjList[i].firstedge = NULL;
    }
    //建立边表（头插法）
    for (k = 0; k < G->numEdges; k++)
    {
        cout << "输入边（vi,vj）上的顶点序号" << endl;
        cin >> i >> j;
        e = new EdgeNode;
        e->adjvex = j;
        e->next = G->adjList[i].firstedge;
        G->adjList[i].firstedge = e;

        e = new EdgeNode;

        e->adjvex = i;
        e->next = G->adjList[j].firstedge;
        G->adjList[j].firstedge = e;
    }
}

void AdjacencyList::Test() {
    cout << "ALL IS OK." << endl;
}

void AdjacencyList::ShowALGraph(GraphAdjList *G) {
    for (int i = 0; i < G->numVertexes; i++)
    {
        cout << "顶点" << i << ": " << G->adjList[i].data << "--firstedge--";
        edgeNode *p = new edgeNode;
        p = G->adjList[i].firstedge;
        while (p)
        {
            cout << p->adjvex << "--Next--";
            p = p->next;
        }
        cout << "--NULL" << endl;
    }

}

void AdjacencyList::DFS(GraphAdjList *G, int i) {
    EdgeNode *p;
    visted[i] = 1;
    cout << G->adjList[i].data << "--";
    p = G->adjList[i].firstedge;
    while (p)
    {
        if (!visted[p->adjvex])
        {
            //递归访问
            DFS(G, p->adjvex);
        }
        p = p->next;
    }

}

void AdjacencyList::DFSTraverse(GraphAdjList *G) {
    //初始化所有顶点都没有访问过
    cout<<"深度优先遍历结果为："<<endl;
    for (int i = 0; i < G->numVertexes; i++)
    {
        visted[i] = 0;
    }
    for (int i = 0; i < G->numVertexes; i++)
    {
        if (visted[i] == 0)
        {
            DFS(G, i);
        }
    }
}


int main() {

    AdjacencyList adjacencyList;
    GraphAdjList *GA = new GraphAdjList;
    adjacencyList.Test();
    adjacencyList.CreateALGraph(GA);
    adjacencyList.ShowALGraph(GA);
    adjacencyList.DFSTraverse(GA);
    return 0;
}



以这张图为基准输入

运行结果

广度优先遍历（BFS）

广度优先遍历，又称广度优先搜索，缩写BFS

如果说深度优先遍历是相当于树的前序遍历，那么，广度优先遍历就相当于树的层序遍历。

以上面那张图为例就是，ABFCIGEDH

代码实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
 void AdjacencyList::BFSTraverse(GraphAdjList *G) {

    EdgeNode *p;
    queue<int> Q;
    for (int i = 0; i < G->numVertexes; i++)
    {
        visted[i] = 0;
    }
    cout << "广度优先遍历结果为：";
    for (int i = 0; i < G->numVertexes; i++)
    {
        if (visted[i] == 0)
        {
            visted[i] = 1;
            cout << G->adjList[i].data << "--";
            Q.push(i);
            while (!Q.empty())
            {
                Q.front()=i;
                Q.pop();
                p = G->adjList[i].firstedge;
                while (p)
                {
                    if (visted[p->adjvex] == 0)
                    {
                        visted[p->adjvex] = 1;
                        cout << G->adjList[p->adjvex].data << "--";
                        Q.push(p->adjvex);
                    }
                    p = p->next;
                }
            }
        }
    }
}

完整代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
 //
// Created by 烟雨迷离半世殇 on 2018/11/21.
//

#include <iostream>
#include <queue>

using namespace std;

//访问标志的数组,为1表示访问过，为0表示未被访问
int visted[100];
//边表结点
typedef struct EdgeNode {
    //顶点对应的下标
    int adjvex;
    //指向下一个邻接点
    struct EdgeNode *next;
} edgeNode;

//顶点表结点
typedef struct VertexNode {
    //顶点数据
    char data;
    //边表头指针
    edgeNode *firstedge;
} VertexNode, AdjList[100];

//集合
typedef struct {
    AdjList adjList;
    //顶点数和边数
    int numVertexes, numEdges;
} GraphAdjList;

class AdjacencyList {
public:

    void CreateALGraph(GraphAdjList *G);

    void ShowALGraph(GraphAdjList *G);

    void DFS(GraphAdjList *G, int i);

    //深度优先遍历
    void DFSTraverse(GraphAdjList *G);

    //广度优先遍历
    void BFSTraverse(GraphAdjList *G);

    void Test();


};

void AdjacencyList::CreateALGraph(GraphAdjList *G) {
    int i, j, k;
    edgeNode *e;
    cout << "输入顶点数和边数" << endl;
    //输入顶点数和边数
    cin >> G->numVertexes >> G->numEdges;
    //读入顶点信息，建立顶点表
    for (i = 0; i < G->numVertexes; i++)
    {
        //输入顶点信息
        cin >> G->adjList[i].data;
        //将边表置为空表
        G->adjList[i].firstedge = NULL;
    }
    //建立边表（头插法）
    for (k = 0; k < G->numEdges; k++)
    {
        cout << "输入边（vi,vj）上的顶点序号" << endl;
        cin >> i >> j;
        e = new EdgeNode;
        e->adjvex = j;
        e->next = G->adjList[i].firstedge;
        G->adjList[i].firstedge = e;

        e = new EdgeNode;

        e->adjvex = i;
        e->next = G->adjList[j].firstedge;
        G->adjList[j].firstedge = e;
    }
}

void AdjacencyList::Test() {
    cout << "ALL IS OK." << endl;
}

void AdjacencyList::ShowALGraph(GraphAdjList *G) {
    for (int i = 0; i < G->numVertexes; i++)
    {
        cout << "顶点" << i << ": " << G->adjList[i].data << "--firstedge--";
        edgeNode *p = new edgeNode;
        p = G->adjList[i].firstedge;
        while (p)
        {
            cout << p->adjvex << "--Next--";
            p = p->next;
        }
        cout << "--NULL" << endl;
    }

}

void AdjacencyList::DFS(GraphAdjList *G, int i) {
    EdgeNode *p;
    visted[i] = 1;
    cout << G->adjList[i].data << "--";
    p = G->adjList[i].firstedge;
    while (p)
    {
        if (!visted[p->adjvex])
        {
            //递归访问
            DFS(G, p->adjvex);
        }
        p = p->next;
    }

}

void AdjacencyList::DFSTraverse(GraphAdjList *G) {
    //初始化所有顶点都没有访问过
    cout << "深度优先遍历结果为：" << endl;
    for (int i = 0; i < G->numVertexes; i++)
    {
        visted[i] = 0;
    }
    for (int i = 0; i < G->numVertexes; i++)
    {
        if (visted[i] == 0)
        {
            DFS(G, i);
        }
    }
}

void AdjacencyList::BFSTraverse(GraphAdjList *G) {

    EdgeNode *p;
    queue<int> Q;
    for (int i = 0; i < G->numVertexes; i++)
    {
        visted[i] = 0;
    }
    cout << "广度优先遍历结果为：";
    for (int i = 0; i < G->numVertexes; i++)
    {
        if (visted[i] == 0)
        {
            visted[i] = 1;
            cout << G->adjList[i].data << "--";
            Q.push(i);
            while (!Q.empty())
            {
                Q.front()=i;
                Q.pop();
                p = G->adjList[i].firstedge;
                while (p)
                {
                    if (visted[p->adjvex] == 0)
                    {
                        visted[p->adjvex] = 1;
                        cout << G->adjList[p->adjvex].data << "--";
                        Q.push(p->adjvex);
                    }
                    p = p->next;
                }
            }
        }
    }
}


int main() {

    AdjacencyList adjacencyList;
    GraphAdjList *GA = new GraphAdjList;
    adjacencyList.Test();
    adjacencyList.CreateALGraph(GA);
    adjacencyList.ShowALGraph(GA);
    adjacencyList.BFSTraverse(GA);
    return 0;
}

以下面这张图为例

运行截图

DFS和BFS的非递归实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
void DFS(Node root)   //非递归实现
{
    stack<Node> s;
    root.visited = true;
    printf("%d ", root.val);     //访问
    s.push(root);              //入栈
    while (!s.empty())
    {
        Node pre= s.top();          //取栈顶顶点
        int j;
        for (j = 0; j < pre.adjacent.size(); j++)  //访问与顶点i相邻的顶点
        {
            Node cur = pre.adjacent[j];
            if (cur.visited == false)
            {
                printf("%d ", cur.val);     //访问
                cur.visited = true;
                s.push(cur);           //访问完后入栈
                break;               //找到一个相邻未访问的顶点，访问之后则跳出循环
            }
        }
        //对于节点4，找完所有节点发现都已访问过或者没有临边，所以j此时=节点总数，然后把这个4给弹出来
        //直到弹出1，之前的深度搜索的值都已弹出，有半部分还没有遍历，开始遍历有半部分
        if (j == pre.adjacent.size())                   //如果与i相邻的顶点都被访问过，则将顶点i出栈
            s.pop();
    }
}

void BFS(Node root) {
    queue<Node> q;
    root.visited = true;
    printf("%d ", root.val);     //访问
    q.push(root);              //入栈
    while (!q.empty()) {
        Node pre = q.front();
        q.pop();
        for (Node cur : pre.adjacent) {
            if (cur.visited == false) {
                printf("%d ", cur.val);     //访问
                cur.visited = true;
                q.push(cur);
            }
        }
    }
}